FIGURAS EQUIVALENTES

9. Relaciones geométricas

Para la construcción y réplica de distintas figuras o piezas, se ha de conocer las relaciones geométricas que pueden darse. Por tanto, es muy oportuno saber definir y distinguir elementos que tengan las características de: igualdad, equivalencia, semejanza, escalas y simetría.

Aunque el conocimiento de todas estas relaciones es muy conveniente, el apartado de ESCALAS (normalización, construcción y empleo), es de suma importancia sobre todo para los dibujos de aplicación industrial.

Distribución:

1. Igualdad.
2. Equivalencia.
3. Semejanza.
4. Escalas.
5. Simetrías.

Desarrollo

---

9.1. Igualdad

Se considera que dos figuras planas son IGUALES, cuando sus lados y ángulos están dispuestos de tal forma que, superponiendo una figura sobre la otra, ambas coinciden.

A menudo es necesario trasladar una figura plana de un lugar a otro, por lo que es conveniente conocer algún procedimiento para realizar una “copia” de esa figura.

Los procedimientos existentes son:

• Por triangulación
• Por perpendiculares
• Por arcos o de rodeo
• Por radiación

.

9.2. Equivalencias

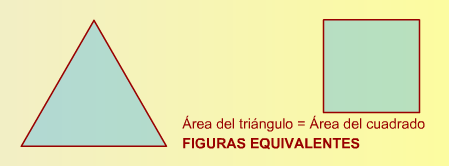
Dos figuras son equivalentes cuando teniendo diferente forma tienen igual superficie, es decir, el área de las dos figuras es igual.

De la misma forma, dos cuerpos geométricos son equivalentes cuando, teniendo 

Figuras equivalentes

Podemos llamar figuras equivalentes a aquellas que tienen la misma area.

formas distintas, sus volúmenes son iguales.

Existen numerosos procedimientos para buscar figuras equivalentes a otras, pero nos centraremos en las siguientes propuestas:

• Triángulo equivalente a un polígono irregular dado
• Cuadrado equivalente a un rectángulo dado

9.3. Semejanza

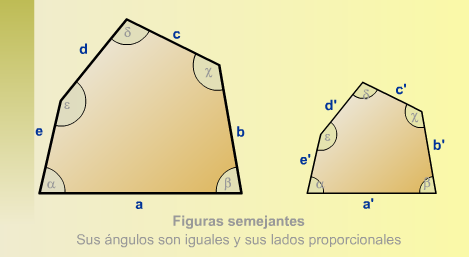
Se dice que dos figuras son semejantes cuando los ángulos homólogos (de la misma forma) son iguales mientras que los lados homólogos son proporcionales.

9.4. Escalas

A menudo nos encontramos que tenemos que representar dibujos excesivamente grandes para poderlos situar en láminas o planos. Otras veces, el objeto es demasiado pequeño y no habrá condiciones suficientes para que quede bien representado. En estos casos es necesario aplicar una escala.

Por lo comentado, tenemos escalas de reducción y escalas de ampliación. La escala natural, E=1:1 (se dice, escala uno es a uno), representa los objetos con las medidas reales.

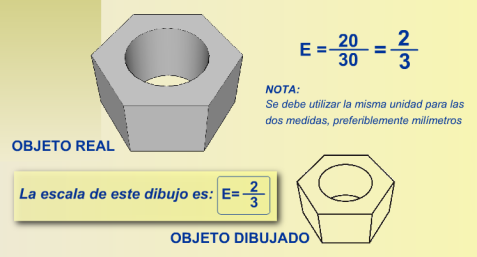
La escala es la relación existente entre las dimensiones de un dibujo y las dimensiones reales del objeto representado.

.

En el apartado de escalas hay varios conceptos que debemos tener claros:

• Tipos de escala
• Cambios de escala
• Escalas normalizadas
• Escalas gráficas

.

9.5. Simetrías

Se dice que dos figuras son simétricas respecto a un punto (simetría central o simetría radial) o respecto a una recta (simetría axial) cuando al girar una de las figuras sobre el punto o la recta (llamada eje de simetría) respectivamente, ambas figuras coinciden.

.

Como se ha comentado, tenemos dos tipos de simetría:

• Simetría central o simetría radial
• Simetría axial

Una vez tenidas en cueta estas definiciones , nos centraremos en la composición del diseño  basandonos el la composición de triángulos semejantes entre ellos.

En el caso de los triángulos podemos decir que Triángulos equivalentes: si tienen la misma base, han de tener la misma altura para que sus áreas sean iguales. Por tanto basta con hacer una horizontal (paralela a la base) y por cualquier punto de esta recta colocar el vértice del nuevo triángulo.

Triangulos

Teniendo en cuenta esto, lo tomaremos como modelo para nuestro diseño para una marca de moda, donde podemos observar como se cumple la equivalencia.

El sistema diédrico aplicado al diseño gráfico

¿Que significa sistema diédrico?

El sistema diédrico es un método de representación geométrico de los elementos del espacio tridimensional sobre un plano, es decir, la reducción de las tres dimensiones del espacio a las dos dimensiones del plano, utilizando una proyección ortogonal sobre dos planos que se cortan perpendicularmente. Para generar las vistas diédricas, uno de los planos se abate sobre el segundo.
Es un método gráfico de representación que consiste en obtener la imagen de un objeto (en planta y alzado), mediante la proyección de haces perpendiculares a dos planos principales de proyección, horizontal (PH) y vertical (PV). El objeto queda representado por su vista frontal (proyección en el plano vertical) y su vista superior (proyección en el plano horizontal); también se puede representar su vista lateral, como proyección auxiliar.

Si se prescinde de la línea de tierra, se denomina sistema diédrico directo.

Planos proyectantes principales
Los dos planos proyectantes principales son el Horizontal y el Vertical. Su intersección se denomina Línea de tierra.

• Plano Horizontal (PH): contiene la proyección horizontal o planta Está subdividido por la Línea de tierra (LT) en: Plano Horizontal Posterior (detrás) y Plano Horizontal Anterior (delante).
• Plano Vertical (PV): contiene la proyección vertical o alzado. Está subdividido por la Línea de Tierra en: Plano Vertical Superior (arriba) y Plano Vertical Inferior (abajo).

Las tres proyecciones ortogonales principales: frontal, superior y lateral (alzado, planta y perfil).

Normalmente, sólo se usan los planos PH y PV, que se cortan en la Línea de tierra (LT) dando origen a una subdivisión del espacio en cuatro ángulos diedros o cuadrantes.
También se utiliza, como plano auxiliar, el denominado:

• Plano de Perfil (PP): contiene la proyección lateral izquierda (o derecha).

Planos bisectores

Los dos planos bisectores son aquellos que dividen a los cuadrantes en dos octantes de 45º cada uno. El primer bisector está en el primero y tercer cuadrante y el segundo bisector en el segundo y cuarto cuadrante.
Para representar en dos dimensiones (sobre un papel) las vistas principales en el sistema diédrico, se realiza un abatimiento, que consiste en girar, tumbar, o abatir un plano principal de tal manera que el Plano Horizontal (PH) se superponga al Plano Vertical (PV).

Representación de un punto
Un punto situado en el espacio se representa mediante sus dos proyecciones (a modo de sombras) sobre los planos principales: proyección horizontal y proyección vertical.

Cota

Se denomina cota de un punto del espacio a la distancia entre él y su proyección en el plano horizontal, o lo que es lo mismo la distancia entre la proyección vertical y la línea de Tierra (LT). Es decir, su distacia en el eje Z.

Alejamiento

Se denomina alejamiento de un punto del espacio a la distancia entre él y su proyección en el plano vertical, que equivale a la distancia entre la proyección horizontal y la línea de Tierra (LT). Es decir, su distancia en el eje Y.

Lateralidad

Se denomina lateralidad de un punto del espacio a su situación (derecha o izquierda) respecto a la línea de tierra (LT). Es decir, su distancia en el eje X.

Determinación por coordenadas

Un punto puede determinarse por coordenadas. El origen de este sistema será la intersección de los planos principales: horizontal, vertical y de perfil.

• El eje X está determinado por la recta intersección de los planos horizontal y vertical, es decir, sobre la Línea de tierra.
• El eje Y está determinado por la recta intersección de los planos horizontal y de perfil.
• El eje Z está determinado por la recta intersección de los planos vertical y de perfil.

Representación de una recta
Una recta está definida cuando se conocen sus dos proyecciones, horizontal y vertical. La proyección de una recta sobre un plano es otra recta, formada por la proyección de todos los puntos de ella. Conociendo las parejas de proyecciones de dos puntos de una recta, se obtiene la proyección uniéndolos.

Trazas de una recta

Las trazas de una recta son los puntos de intersección con los planos principales (PV y PH)
Representación de un plano
Un plano está definido mediante sus dos trazas: la vertival y lahorizontal. Las trazas de un plano son las rectas de intersección con los planos principales (PV y PH).
Una recta  pertenece a un plano, si la traza vertical de la recta es un punto de la traza vertical del plano y, además, la traza horizontal de la recta es un punto de la traza horizontal del plano.

Abatimientos

Para obtener, en verdadera magnitud, la representación de una figura contenida en un plano cualquiera, se abate dicho plano sobre uno de los principales.

Representación de un volumen geométrico
Un cuerpo geométrico se representa mediante la proyección de sus aristas, sus generatrices extremas, o su contorno (esfera). Las aristas o generatrices más próximas al punto de vista se representan como segmentos de trazo continuo, y las posteriores, u ocultas, mediante segmentos de trazo discontinuo. Las zonas seccionadas se indican mediante trazos paralelos inclinados.
Representación de una circunferencia

La proyección de una circunferencia es, generalmente, una elipse. Será otra circunferencia semejante si está contenida en un plano paralelo a uno principal. Puede ser un segmento si está de perfil respecto de un plano principal, siendo su longitud la del diámetro.
Diferentes sistemas
Según como estén reflejadas las proyecciones en el plano del dibujo, existen dos sistemas de representación:

• Sistema europeo: Las proyecciones se recogen tras el objeto. Son vistas en el primer cuadrante.
• Sistema americano: Las proyecciones se reflejan desde el objeto. Son vistas en el tercer cuadrante.

Aunque en ambos sistemas las proyecciones (representaciones del objeto) son exactamente las mismas, su disposición en el plano del dibujo es la inversa.




Una vez que ya sabemos la teoria, procederemos a crear nuestra propia representación, para mas tarde crear nuestro diseño aplicado a las matemáticas.

Lo que hemos hecho , ha sido proyectar cada uno de sus lados partiendo de unos ejes, atravez de paralelas de cada uno de sus lados siendo cortados estos por los vertices que daran forma a la proyección de la figura.

Una vez tenemos la formula matemática procederemos a la creación de la composición de diseño gráfico con componentes matemáticos, como podemos observar en este cartel publicitario.

Homologia

En este apartado  veremos la homologia aplicada a diseños gráficos, para ello debemos de entender que es la homología y en que consiste para finalmente crear la composición gráfica.

Homología

La proyección de dos figuras planas que se encuentran en planos distintos, desde un punto exterior a los dos planos. Muy utilizada para hallar secciones de cuerpos como piramides y conos.

Para la creación de la composición que encontraremos al final de todo , seguiremos un proceso detallado, para que se entienda la homologación que realizamos con cada figura.

Para realizar esta composición realizaremos las figuras geométricas que deseemos , a continuación  lla linea de eje , y el punto 0, una vez tengamos esto, trazamos una recta que sea paralela a la figura de modo que los dos vértices inferiores queden unidos al eje y formen los puntos F=F´ , M=M´ desde estos puntos lanzaremos unas lineas que se unan en la linea L y desde esta al punto 0 . Por otro lado uniremos los vértices de las dos figuras con el punto 0 mediante rectas, y ahora es cuando podemos observar las intersecciones que forman las lineas que parten de la linea eje y las que parten de los vértices, en estas intersecciones crearemos los puntos A,B,C,D que darán lugar a una proyección de la figura inicial , proporcionándonos el resultado deseado.




Una vez que hemos conseguido el resultado buscado podemos crear la composición aplicada al diseño gráfico, mostrando que las matemáticas y el diseño son totalmente compatibles nuevamente, como se muestra en esta portada de cd para el grupo The Marmales en el que aplicamos el ejercicio realizado.